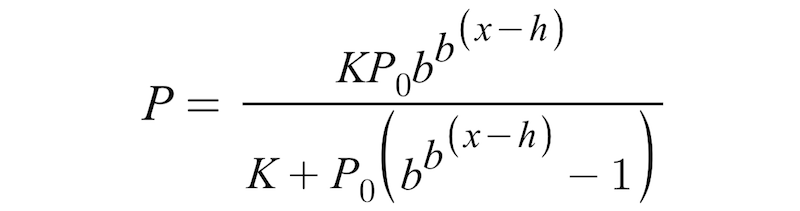Stephen Farrington -- World News Trust
Jan. 20, 2018
A lot of sensational headlines over the past few days have announced the “crash of bitcoin,” the “bursting of the bubble,” the “beginning of the end” for cryptocurrencies. They’re wrong, and here’s why.
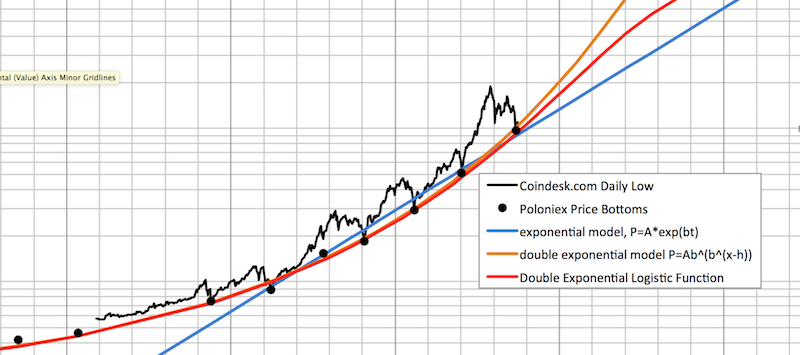
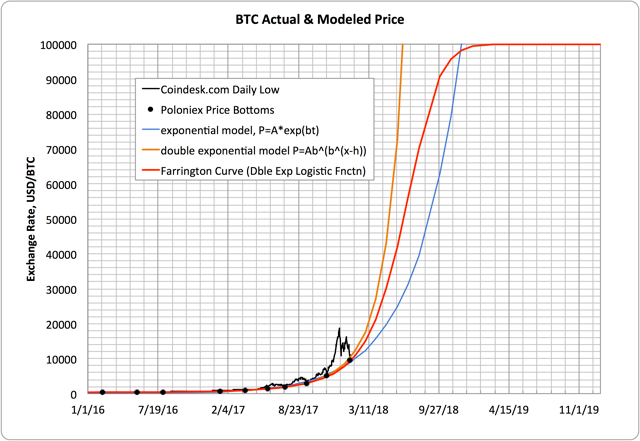
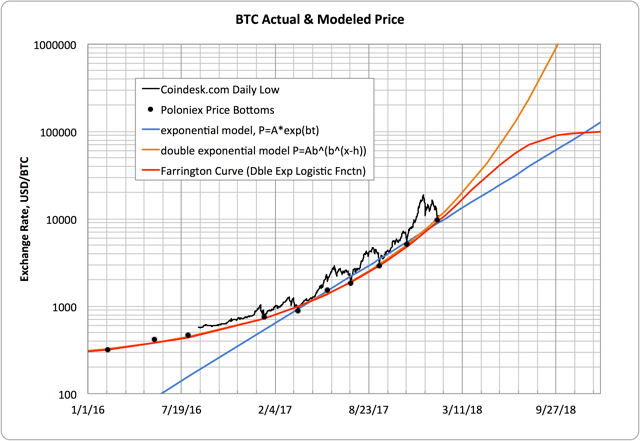
Below are two plots showing a model I developed to predict bitcoin price based on fitting a double exponential logistic function to bitcoin price bottoms. It’s a nearly perfect fit to the data, it precisely predicts the most recent low, and it suggests an explosive upside still ahead. The first plot shows the phenomenon on a linear price scale to convey the magnitude of where we are with respect to the underlying adoption curve explained in more detail below. The second plot uses a logarithmic price scale to zoom in the detail and to emphasize how an exponential model is insufficient to capture the growth that’s been happening.


For the price bottoms shown as black dots, I used BTC-USDT data from Poloniex, simply because it was easy to scrape from their charts. I know USDT isn’t USD — if you beat me up about it you’re completely missing the point. The black line represents daily lows in real US dollars reported by CoinDesk for comparison.
I experimented with three models to try to fit the data. The blue line is a simple exponential growth curve. Exponential functions plot as a straight line on logarithmic axes, and I included this model to show that the an assumption of exponential growth is insufficient to capture the accelerating ascent of bitcoin’s value. This point is best illustrated on the semi-log plot, where the blue exponential model appears as a straight line, while bitcoin price history curves upward.
The orange line depicts double exponential growth. Double exponential is when the rate of exponential growth is itself growing at a exponential rate. The double exponential model nails the bitcoin price bottoms, shown most precisely on the logarithmic plot.
My point is that, while the price peaks have garnered all the attention and characterize all the volatility, the price bottoms indicate reliable double exponential growth, including the value under $10,000 as of Wednesday’s so-called crash.
The value of bitcoin did not crash. It experienced an expected correction back to normal double exponential growth!
The growth of the orange curve can’t last forever. This is where a logistic function, represented by the red line, comes in. Logistic functions are a family of mathematical functions scientists use to describe growth followed by stabilization. They usefully model things like the population of some reptile on an island, or the number of people infected by a virus. Logistic functions make S-shaped curves in which the later end of the curve levels out, accounting for when the lizards eat all the vegetation on the island, or the virus has infected everyone who isn’t immune. Adoption of new technologies tends to follow S-curves, too. It starts slowly with developers, followed by early adopters, and then accelerates as the mainstream picks up on the technology, and finally it peters out as the last of the late adopters eventually straggle on board. For good example S-curves of technology adoption, check out Paulo Caroli’s blog.
Since bitcoin is a new technology, its adoption should follow a familiar S-curve and should be amenable to modeling using a logistic function. “Should” and “does” aren’t always the same thing and, as it turns out, we need a special logistic function. But more on that later.
How does adoption relate to price?
Adoption of bitcoin drives demand for bitcoin, and demand of anything drives its price, especially the price of something for which there is a clearly limited supply. Only 21 million bitcoin will ever come into existnce, over 80% of them have already been mined, the current rate of new bitcoin production is very slow relative to the number in circulation, and true believers in where cryptocurrency is headed won’t give up their bitcoin on an exchange for any amount of fiat currency. Not until we can buy our groceries and pay our rent in cryptos. For these reasons, bitcoin may be one of the purest examples ever of fixed supply. Which suggests that price should almost perfectly reflect demand.
Since we previously established that demand is a reflection of adoption, and now that price is a reflection of demand, it logically follows that price should almost perfectly reflect adoption. Which is why a logistic function should be an appropriate model of bitcoin price growth versus time. Except that every logistic function I’ve ever seen only models exponential growth, which we’ve seen is insufficient to describe bitcoin. I therefore replaced the exponential and logarithm expressions in the logistic function with double exponential and double logarithmic expressions.

Why a double exponential logistic function?
Unlike the spread of a virus or compound interest (which Albert Einstein reportedly called “the most powerful force in the Universe” ), technology growth, especially when network effects are involved, exceeds exponential. Ray Kurweil observed as far back as 2001 that technology growth is often double exponential. The explosive growth of bitcoin, as evidenced in the data, can not be modeled without resorting to a double exponential formulation.
But why model the price bottoms?
Bottoms are points in time when the price was lowest relative to surrounding price movement. I chose bottoms under the hypothesis that the recalcitrance of permanent adopters to part with their bitcoin (unlike speculators, FOMO buyers, and panic sellers) is what constrains supply and thus arrests price drops at a level commensurate with the true adoption curve. The bottoms therefore represet true permanent adoption of bitcoin. In this view of the phenomenon, excursion above a growth curve that passes through the bottoms are the anomalies; the bottoms are what’s normal and predicatable.
For crypto investors, the really fun thing about the double exponential logistic model shown by the red line is that the potential for price growth over the next year is practically immune to the choice of maximum price (the flat spot at the end of the curve). At $100,000 USD, I’ve shown a somewhat arbitrary choice of maximum price. For any terminal value that’s sufficient to approximate the magnitude of upward curvature we’ve already witnessed, the price trajectory over the next several months changes negligibly. If the actual price continues to conform to the double exponential model, we could see BTC easily exceed $50,000 before the end of this year.
Evidence suggests that continued upward movement in the price of bitcoin is not a bubble. The math shows it’s not a so-called “parabolic” movement. (Why do pundits characterize anything non-linear as parabolic?) Bitcoin price seems to follow a double-exponential logistic curve, which should not be surprising given the dynamics of technology adoption, network effects, and macroeconomic theory.
Even at $10,000, the price movement so far is barely past the start of a double exponential S-shaped adoption curve, and it appears to have a long way to go.
Disclaimer: I am not a financial management professional and do not offer financial advice. Seek the advice of a licensed financial professional if you are contemplating an investment in anything, including cryptocurrencies.
***
 Stephen Farrington MS PEStephen Farrington, MS, PE. Entrepreneur, Engineer, Scientist, Deep Generalist. Blockchain and Cryptocurrency Consultant.
Stephen Farrington MS PEStephen Farrington, MS, PE. Entrepreneur, Engineer, Scientist, Deep Generalist. Blockchain and Cryptocurrency Consultant.